Introduction

In this laboratory experience, four main objectives are set: i) learning to read and write input and understand output from basic calculations using the CRYSTAL program; ii) gaining knowledge of the fundamental ingredients underlying computational calculations and examining their effects on the properties of systems; iii) simulating and studying the properties (band structure, density of states, electron charge density) of diverse systems (molecules, metals, ionic and molecular crystals); iv) calculating the energy of a reaction; v) simulating vibrational spectra (IR and Raman).
To achieve the goal of the experiment, the following reaction will be considered:

Na + NH₃ → NaNH₂ + 1/2 H₂

This reaction is of considerable interest in the field of hydrogen production.
Recently, amides of alkali metals together with ligth-weigth metal hydrides have drawn attention as solid-state hydrogen storage materials.
Among them, NaNH₂ is of considerable interest, because of its role in the dehydrogenation of other light metal hydride systems, by forming composite hydrogen storage materials, as NaNH₂-LiBH₄ and others.
We will examine all the compounds taking part to such reaction.

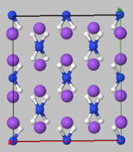
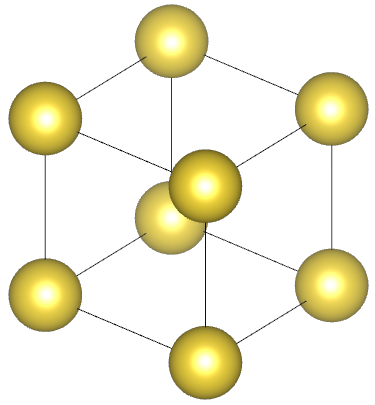
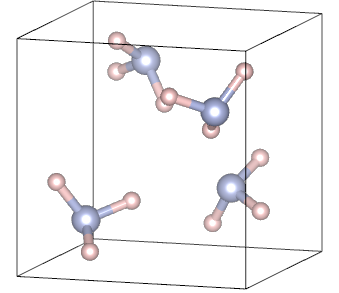
Na: metal	NH₃: molecular crystal

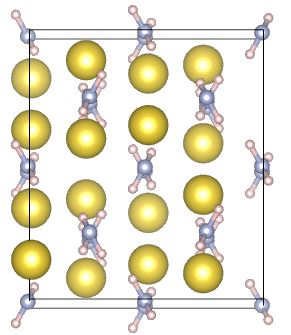
NaNH₂: ionic crystal	H₂: molecule

Figure 1 Rapresentation of the structure of investigated systems

In this initial introductory part of the laboratory, we aim to achieve the first two objectives, namely learning the construction of a CRYSTAL input, the reading of an output and how the choice of the level of theory influences the calculation result by focusing on ammonia molecule.

Figure 2 NH₃ molecule rapresentation.

Construction of a CRYSTAL input

To begin, we first have to learn the main ingredients to construct an input file in CRYSTAL. Below we will give you some basic and fundamental notions, but you can refer to CRYSTAL manual to have in-depth information. Let’s analyse the following CRYSTAL input:

Ammonia molecule
MOLECULE
30
2
1 0. -0.9377 -0.3816
7 0. 0. 0.
END
BASISSET
POB-TZVP
DFT
PBE0-D3
END
MULPOPAN
END

The input can be divided into three main sections: i) geometry section; ii) basis set section; iii) computational parameters, hamiltonian and SCF control section.

i) Geometry specification section

The first line in a CRYSTAL input is the title. It can be whatever you want, but it must be there. In the sample input, it is ‘Ammonia molecule’.

In the second line, instead, system dimensionality is specified through specific keywords: MOLECULE for a 0D system (as in the current case); POLYMER for a 1D system; SLAB for a 2D system; CRYSTAL for a 3D system. Now, we will focus just on the commands related to the present case. Further specification will follow in next sections for other calculations. The keyword MOLECULE requires the specification of point group symmetry label of the molecule (found in CRYSTAL manual) and the number n of non-equivalent atoms, which has to be followed by n rows where the atomic number and fractional coordinates of the atoms of interest. In the current case, ammonia molecule has C_3v symmetry, corresponding to label 30 in CRYSTAL, and 2 non-equivalent atoms are present in the molecule, that are one H atom (atomic number = 1; fractional coordinates 0; -0.9377; -0.3816) and one N atom (atomic number = 7, fractional coordinates 0; 0; 0). Indications on the geometry of a system of interest can be found on different databases as ICSD or CSD.

Additional optional keywords can be added at the end of the geometry section. If none is introduced, simple single point calculation is performed. In the current case, OPTGEOM keyword has been specified, that means that optimization of the input geometry is required. This command has to be followed by END.

ii) Basis set specification section

In the second section, the chosen basis set for the calculation must be specified. It can be done either implicitly or explicitly. Just few pre-defined implicit basis sets are available in CRYSTAL, as pob-tzvp used in the current case. However, if different kinds of basis sets want to be used in the calculation, it is possible to find them in CRYSTAL basis set library. CRYSTAL employs basis sets of atom-centered Gaussian type orbitals, hence a basis set for each non-equivalent atom of the structure has to be specified.

Below a sample input with 6-31d1G basis set for N and 3-1p1G basis set for H is shown.

Ammonia molecule
MOLECULE
30
2
1 0. -0.9377 -0.3816
7 0. 0. 0.
OPTGEOM
END
END
7 4
0 0 6 2. 1.
0.417351E+04 0.183477D-02
0.627458E+03 0.139946D-01
0.142902E+03 0.685866D-01
0.402343E+02 0.232241E+00
0.128202E+02 0.469070E+00
0.439044E+01 0.360455E+00
0 1 3 5. 1.
0.116264E+02 -.114961E+00 0.675797D-01
0.271628E+01 -.169117E+00 0.323907E+00
0.772218E+00 0.114585E+01 0.740895E+00
0 1 1 0. 1.
0.212031E+00 0.100000E+01 0.100000E+01
0 3 1 0. 1.
0.800000E+00 0.100000E+01
1 3
0 0 3 1.0 1.0
.1873113696D+02 .3349460434D-01
.2825394365D+01 .2347269535D+00
.6401216923D+00 .8137573262D+00
0 0 1 0.0 1.0
.1612777588D+00 .1000000000D+01
0 2 1 0.0 1.0
.1100000000D+01 .1000000000D+01
99 0
END
DFT
PBE0-D3
END
MULPOPAN
END

If the basis set is explicitly defined, it must be followed by 99 0 and END and an additional END must be present at the end of the geometry specification section.

iii) Computational parameters, Hamiltonian and SCF control section

In this section, parameters that control the calculation of the Hamiltonian are defined.
In this case, just two keywords are inserted: DFT and MULPOPAN.
The first one opens the possibility to define a specific functional for the calculation, which in our sample calculation is PBE0 with D3 dispersion correction. If DFT keyword is not inserted, HF method will be used. MULPOPAN keyword instead activates the Mulliken population analysis at the end of SCF process.

Other important keywords will be discussed at appropriate points throughout this tutorial.

Figure 3 CRYSTAL opening page.

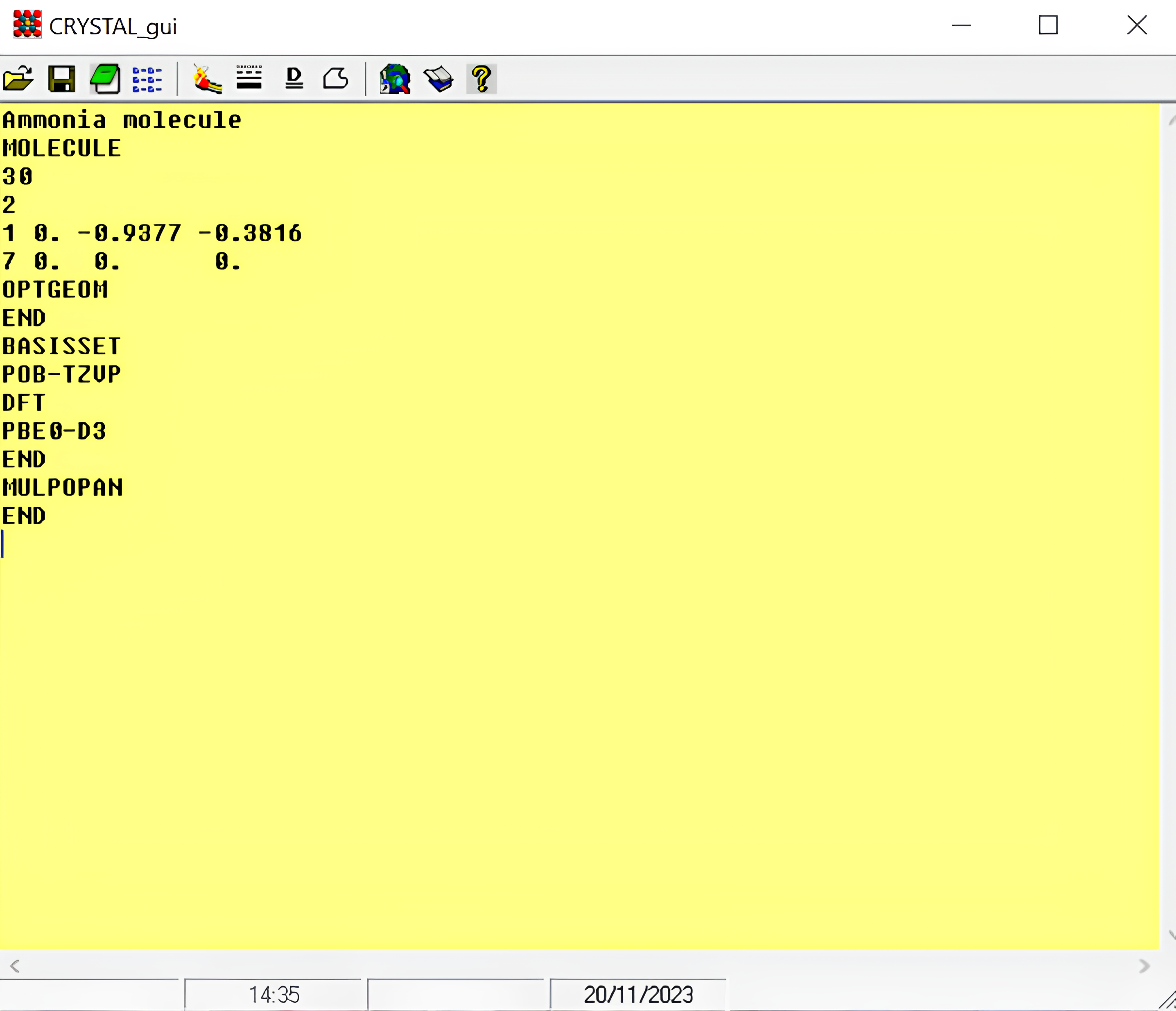
In Figure 2, the opening page of CRYSTAL program is presented. The sample input of ammonia molecule is written. To run a CRYSTAL calculation you will only need to: i) write the input file; ii) save it with d12 extension (filename.d12); iii) (just for CRYSTAL Windows version) push the ‘matchstick’ bottom -the fourth from the left. In the same folder, at the end of the calculation, you will find all the output files.

When you create a file, give it a name so that you can understand what it is related to and do not insert spaces.

Impact of basis set and functional on a calculation

Now we want to verify the effect of basis set and functional choice – the main ingredients of a quantum chemical calculation. First of all, let us have a look to the structure of a standard CRYSTAL calculation.

In the initial part of the output, an analysis of geometry and symmetry is done. The basis set is reported, indicating atom, orbital type and number, exponents and coefficients. The SCF calculation starts. In the output, total energy, band gap and atomic charges are reported for each cycle. When OPTGEOM keyword is specified in the input, geometry optimization is performed by the program that is searching for the atomic coordinates (and cell parameters for periodic systems) that minimize the energy of the system. Each point of optimization is reported in the output, indicating also the value of the parameters that control the progress of optimization process respect to a threshold value. When optimization ends (OPT END), the total energy (including dispersion correction, if you chose it in your calculation) is printed, together with the final band gap (for semiconductors or insulating systems) or Fermi energy level (for conductors). In the end, analysis of final optimized geometry is reported: distance of atoms, Mulliken population analysis, atomic orbitals population and overlap population. An example is reported in Figure 4.

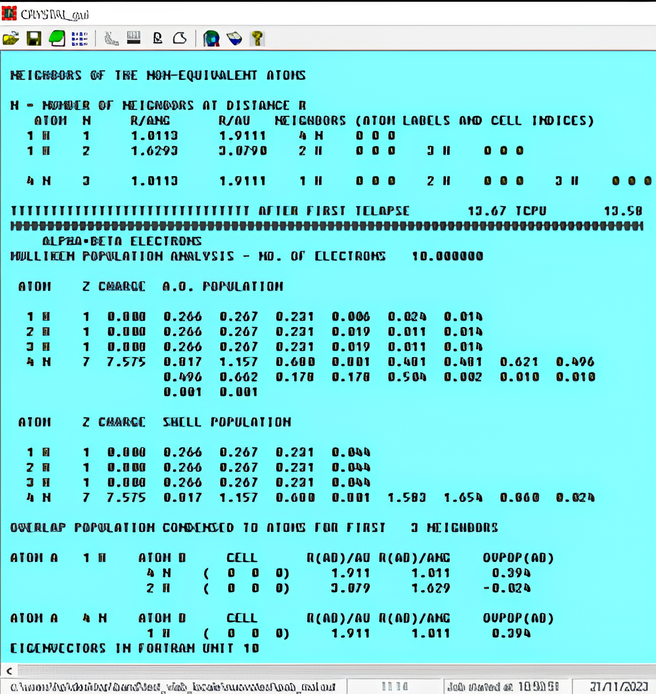
Figure 4 Portion of CRYSTAL output.

Now that we know how to read and interpret a CRYSTAL output, we can compare the resulting outputs of NH₃ molecule optimization calculation performed with the same functional – PBE0-D3 – but with two different basis sets: i) pob-tzvp and ii) 6-31d1G basis set for N and 3-1p1G basis set for H.

How the total energy, N and H Mulliken charges and HOMO-LUMO gap are changing?

Same kind of analysis can be done by changing DFT functional while keeping the same basis set. Considering PBE0-D3, PBE and SVWN functionals, how the total energy, N and H Mulliken charges and HOMO-LUMO gap are changing? Consider 6-31d1G basis set for N and 3-1p1G basis set for H.

Exercise:
Build two tables – one for analyzing the effect of the basis set and one for analyzing the effect of the functional – and fill them with the different obtained results for the above-mentioned parameters.