|
Titanocenes
|
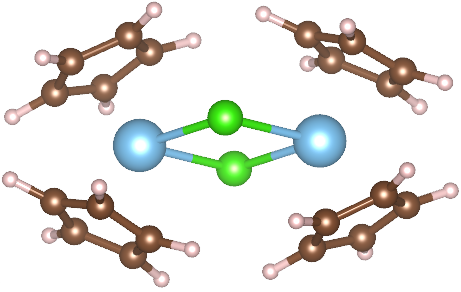
Titanium(III) metallocene compounds provide a very useful visual aid for students learning standard Schlenk vacuum line techniques by changing their colour because of reduction and/or oxidation reactions. In Figure 1, a schematic representation of these mechanism is illustrated. In this tutorial, we are going to perform calculations on dicyclopentadienyltitanium dichloride (Ti(C5H5)2Cl2) system. Three possible crystal structures are found in literature for these Ti complexes: one with P-1 symmetry, one with P1121/n symmetry and one with P21/c symmetry. However, P-1 system and P21/c are related by symmetry, so we are just going to study P1121/n and P21/c crystal structures.
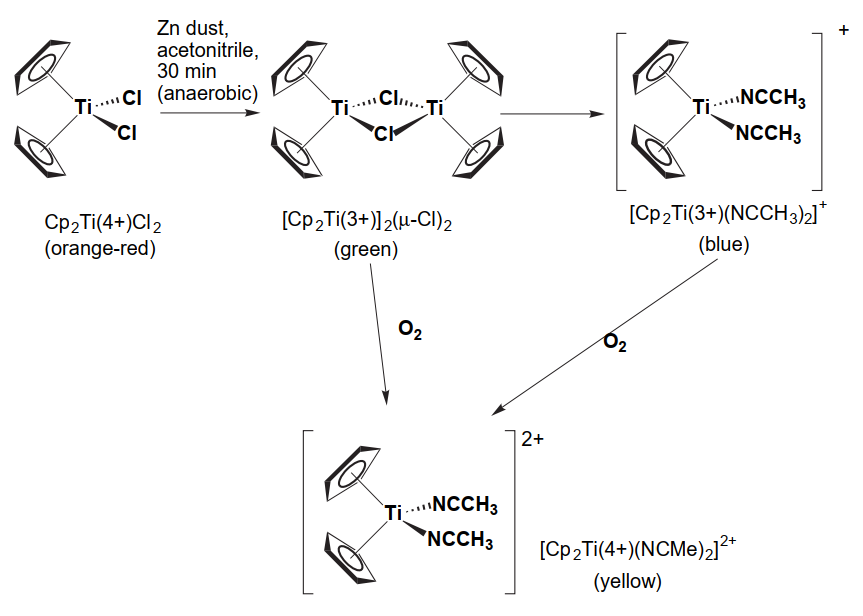
Note that similar analyses to the one we are about to perform can be made also for zirconocenes (Zr(C5H5)2Cl2) and Hf(C5H5)2Cl2.
- Ferromagnetic or antiferromagnetic?
- P1121/n
- Geometry optimization and energy of periodic system
- Extraction of molecular building unit
- Optimization of molecular building unit
- Cohesion energy calculation
- P21/c
Ferromagnetic or antiferromagnetic?
Before proceeding with the study of the complexes of interest, it is essential to analyze their magnetic properties. Specifically, the molecular building unit is a dimer made up of two Ti3+ ions, each with [Ar] 3d1 electronic configuration. What spin states will the two titanium atoms exhibit?
We will now examine not only which spin configuration (up-up or up-down) is most favourable, but also the most favourable occupation of the d orbitals within a single molecular unit in our systems.
Input for ferromagnetic solution:
Magnetism
MOLECULE
1
44
22 1.162553241284E+00 2.844982456061E+00 -9.039939639018E-02
6 4.071117023418E-01 2.017332486939E+00 -2.163761898253E+00
6 2.711534530033E-01 3.656279666568E+00 1.936326012731E+00
6 1.273573930482E+00 2.719558905706E+00 2.289334064714E+00
6 -6.528655779269E-01 2.754953263287E+00 -1.604130670069E+00
6 -7.593891521919E-01 2.948589639120E+00 1.291293724836E+00
6 1.447593507747E+00 2.930609449506E+00 -2.464026593664E+00
6 -2.588211459647E-01 4.113719898909E+00 -1.524318449987E+00
6 -3.853197016462E-01 1.583492483769E+00 1.217206420104E+00
6 8.596818301326E-01 1.444492944059E+00 1.858890916466E+00
6 1.030297149041E+00 4.218900490659E+00 -2.081264784631E+00
17 3.117576152518E+00 1.283450248636E+00 -3.665086797948E-01
17 3.062254488504E+00 4.439124168635E+00 3.426601571728E-01
1 4.192990825152E-01 9.481923014920E-01 -2.356814880739E+00
1 2.895856472887E-01 4.722088836566E+00 2.146245247296E+00
1 2.190383399993E+00 2.948915036587E+00 2.820915939001E+00
1 -1.612087223286E+00 2.350571418120E+00 -1.293877868249E+00
1 -1.685712307026E+00 3.376660235443E+00 9.188596134702E-01
1 2.394338143950E+00 2.675922328440E+00 -2.927569849664E+00
1 -8.551753757306E-01 4.934019458710E+00 -1.133581159920E+00
1 -9.671030897337E-01 7.813415417895E-01 7.707375418129E-01
1 1.414629694419E+00 5.178169357745E-01 1.970718158926E+00
1 1.608734379595E+00 5.133681512054E+00 -2.168858787103E+00
22 5.017507739213E+00 2.877419914628E+00 6.435680160361E-02
6 5.813491823412E+00 1.268588222475E+00 1.591142012444E+00
6 5.864880187391E+00 4.507155175755E+00 -1.414421678760E+00
6 4.891033444724E+00 3.778706915095E+00 -2.141090302506E+00
6 6.846425022771E+00 2.206359608683E+00 1.405726684118E+00
6 4.748002258033E+00 1.934421030444E+00 2.245581767110E+00
6 6.410925832089E+00 3.456628245008E+00 1.910881143890E+00
6 6.595697807800E+00 2.349337960363E+00 -1.647739463739E+00
6 6.923545124344E+00 3.626322561307E+00 -1.127487163813E+00
6 5.349971251781E+00 2.456476546503E+00 -2.294065545008E+00
6 5.123192085564E+00 3.275085801515E+00 2.451152649471E+00
1 5.835204480992E+00 2.194222106360E-01 1.309635938437E+00
1 5.809546916169E+00 5.558998241298E+00 -1.147988524677E+00
1 3.963243658838E+00 4.182795559847E+00 -2.530510056189E+00
1 7.814690605017E+00 2.002551587129E+00 9.575875857935E-01
1 3.812678377153E+00 1.477717428428E+00 2.549888018285E+00
1 6.978744420560E+00 4.383340341554E+00 1.910377027917E+00
1 7.207787637978E+00 1.453468683198E+00 -1.584625008047E+00
1 7.838281324639E+00 3.884337700718E+00 -6.013487591122E-01
1 4.824822658394E+00 1.648779195918E+00 -2.794999132332E+00
1 4.517455676740E+00 4.047185012307E+00 2.916005611346E+00
BASISSET
SOLDEF2MSVP
DFT
SPIN
PBESOL03C
END
MAXCYCLE
300
ATOMSPIN
2
1 1
24 1
FDOCCUP
2
1 8 3
1 0 0 0 0
0 0 0 0 0
24 8 3
1 0 0 0 0
0 0 0 0 0
TOLINTEG
8 8 8 8 16
MULPOPAN
END
ATOMSPIN keyword sets the atomic spin to compute atomic densities. Since in this first example we are interested in simulating a ferromagnetic solution, we set both Ti atoms with spin-up.
FDOCCUP keyword allows to define an initial guess of d orbitals occupation. An accurate description of its use can be found in CRYSTAL23 manual. Here we will only mention the order of d orbitals that is as follows: z2, xz, yz, x2 - y2, xy. (e.g. in the sample input, we occupy the z2 orbital with one electron with spin-up for both Ti atoms). Please, note that this complex is a tetrahedral coordination complex and crystal field splitting in tetrahedral complexes is reported in Figure 2.
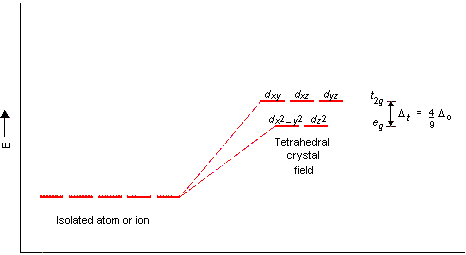
Figure 2 Crystal field splitting for tetrahedral complexes.
The same kind of input can but constructed for the antiferromagnetic solution inserting:
ATOMSPIN
2
1 1
24 -1
FDOCCUP
2
1 8 3
1 0 0 0 0
0 0 0 0 0
24 8 3
0 0 0 0 0
1 0 0 0 0
In this way, with ATOMSPIN keyword we specify that the two Ti atoms have opposite spin states and with FDOCCUP we occupy z2 orbital with one electron with spin-up for the first Ti and with one electron with spin-down for the second Ti.
Exercise: perform the calculations reported above, occupying also different d orbitals, fill the table reported below and compare the results: which configuration is the most stable one - ferromagnetic or antiferromagnetic? Which d-orbitals occupation is the most favourable?
| 10000 | 01000 | 00100 | 00010 | 00001 | |
| z2 | xz | yz | x2 - y2 | xy | |
| E (a.u.) |
| 10000 | 01000 | 00100 | 00010 | 00001 | |
| z2 | xz | yz | x2 - y2 | xy | |
| E (a.u.) |
P1121/n
Geometry optimization and energy of periodic system
Let’s start optimizing crystal geometry for P1121/n system and computing its energy.
In order to do so, we will exploit composite method, a new feature implemented in CRYSTAL23 code, helpful for speed-up the calculation and to take directly into account basis set superposition error (BSSE) correction. Specifically, in our case, we are going to use PBESOL03c functional with SOLDEF2MSVP small basis set.
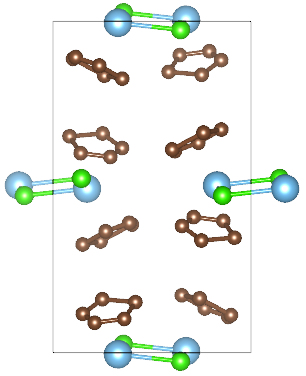
Figure 2 Crystal structure of P1121/n system. (H atoms are not represented)
Input:
P1121/n system
CRYSTAL
1 0 0
P 1 1 21/n
13.571 8.172 8.112 90
22
22 0.4952 0.1724 0.171900000000001
17 -0.4739 -0.1397 0.143800000000001
6 0.3865 0.136800000000001 0.398400000000001
6 0.3357 8.30000000000004E-02 0.240300000000001
6 0.3267 0.2401 0.150000000000001
6 0.366499999999999 0.3422 0.266100000000001
6 0.3921 0.2791 0.385500000000001
6 -0.3472 0.2506 8.39000000000015E-02
6 -0.3387 0.1625 0.250700000000001
6 -0.3826 0.275699999999999 0.348900000000001
6 -0.4093 0.3906 0.289300000000001
6 -0.3979 0.4014 0.140100000000001
1 0.408708219671705 5.57893112461423E-02 0.482993008300583
1 0.324989847795742 -3.80154174020452E-02 0.236651915164343
1 0.292374203512261 0.262117014688609 4.31969642141938E-02
1 0.374495114778143 0.463763755442491 0.261577245668178
1 0.426742888895243 0.342820137859334 0.47334694679353
1 -0.325584939525433 0.25403288295857 -0.033900432018043
1 -0.305724794284826 5.93267140244128E-02 0.287448561319846
1 -0.389010011999691 0.234323687234821 0.46441668220971
1 -0.452489675005483 0.478177171899038 0.336120859914934
1 -0.41126123187611 0.481196030755008 4.93534986094891E-02
MODISYMM
4
1 1
2 2
3 1
4 2
OPTGEOM
END
BASISSET
SOLDEF2MSVP
DFT
SPIN
PBESOL03C
END
SHRINK
8 8
MAXCYCLE
300
THREDIIS
0.01
FMIXING
98
ATOMSPIN
4
1 1
2 -1
3 1
4 -1
FDOCCUP
2
1 8 3
0 0 0 1 0
0 0 0 0 0
2 8 3
0 0 0 0 0
0 0 0 1 0
TOLINTEG
8 8 8 8 16
MULPOPAN
EXCHSIZE
4280706
END
In the first part, geometry of the system is specified (space group specification, minimal set of lattice parameters, number of irreducible atoms in the unit cell followed by their atomic number and fractional coordinates).
In the previous exercise, you should have found that the most stable spin configuration is antiferromagnetic and the most favourable d-orbitals occupation is to place the unpaired electron in x2-y2 orbitals. Therefore, here MODISYMM keyword is inserted to differentiate Ti atoms so that it is possible to set the unpaired electron of one Ti with spin up and the other with spin down. To do this, it is first necessary to modify the symmetry. Moreover, full geometry optimization is requested (both atomic coordinates and cell parameters).
Tolerances on integrals are set to 10-8 for the first four criteria and 10-16 for the last one (TOLINTEG 8 8 8 8 16). The convergence criterion on energy for SCF is set to 10-10 (TOLDEE 10). Furthermore, Mulliken population analysis is requested (MULPOPAN). Shrinking factor is set to 8 8, while FMIXING to 98 to help the correct electron distribution, together with threshold to postpone activation of DIIS (THREDIIS). In order to correctly describe the system as antiferromagnetic, two more steps are required after MODISYMM: i) activate the keyword ATOMSPIN, specifying the spin of atoms of interest; ii) activate FDOCCUP keyword to correctly distribute alpha and beta electrons in d orbitals of Ti.
At the end of the calculation, compare the final optimized lattice parameters at different levels of theory with the experimental ones (a = 13.571, b= 8.172, c= 8.112, beta= 90) to verify their agreement and take note of the final energy that will be needed to calculate the cohesion energy.
Note: this calculation is very time consuming, so in case you cannot run it, precalculated output is provided (p112n.out).
Extraction of molecular building unit
In order to calculate the cohesion energy of a molecular crystal, it is necessary to compute the total energy of the building unit, that is simply the energy of the extracted molecule recognized in the cell, without relaxing it.
Input:
P1121/n – extr. molecule
EXTERNAL
RAYCOV
2
22 1.8
17 1.3
MOLECULE
1
1 0 0 0
MODISYMM
2
1 1
24 2
BASISSET
SOLDEF2MSVP
DFT
SPIN
PBESOL03C
END
MAXCYCLE
300
THREDIIS
0.01
FMIXING
98
ATOMSPIN
2
1 1
24 -1
FDOCCUP
2
1 8 3
0 0 0 1 0
0 0 0 0 0
24 8 3
0 0 0 0 0
0 0 0 1 0
TOLINTEG
8 8 8 8 16
MULPOPAN
END
The input is substantially the same reported for the periodic system, except for few things:
- EXTERNAL keyword to import the geometry of previously optimized crystal structure from f34 file;
- RAYCOV to specify new covalent radii, which plays a crucial role in extracting the correct building unit
- MOLECULE for molecule extraction
Optimization of molecular building unit
In this case, we will use the same CRYSTAL input used for molecule extraction, with the addition of OPTGEOM keyword.
Input:
P1121/n – opt molecule
EXTERNAL
…
OPTGEOM
END
…
Cohesion energy calculation
Now that we have all the ingredients, we can calculate cohesion energy for P1121/n crystal.
Calculate the binding energy (Ebinding = Ecrystal/n – Emolecule), the relaxation energy (Erelax = Eoptmolecule – Emolecule) and the final cohesion energy according to the formula reported above.
P21/c
Geometry optimization and energy of periodic system
Let’s now optimize crystal geometry for P21/c system and compute its energy.
We will use the same computational methos exploited before for P1121/n system.
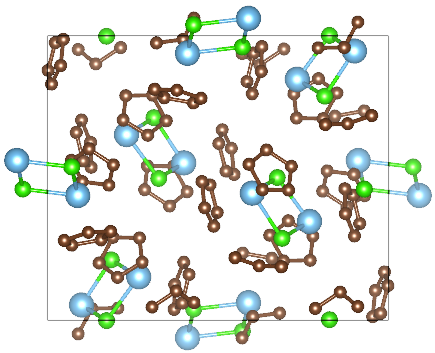
Figure 3 Crystal structure of P21/c system. (H atoms are not represented)
Input:
P21/c
CRYSTAL
0 0 0
14
13.422 15.666 13.083 94.21
66
22 0.24557 0.100330000000001 5.32600000000006E-02
22 0.449410000000003 0.267920000000001 0.152660000000001
22 -9.05199999999991E-02 8.92500000000005E-02 0.438440000000002
6 0.273500000000001 -1.23000000000006E-02 0.1695
6 0.201900000000001 -3.92000000000005E-02 0.1045
6 0.2402 -4.71000000000002E-02 1.25999999999999E-02
6 0.335100000000001 -0.0232 2.43999999999992E-02
6 0.357400000000001 -2.40000000000072E-03 0.1213
6 0.156300000000001 0.142000000000001 -9.87000000000002E-02
6 9.47000000000005E-02 0.090500000000001 -4.82999999999994E-02
6 7.22000000000004E-02 0.1303 4.09000000000003E-02
6 0.119600000000001 0.206800000000001 4.23000000000001E-02
6 0.170500000000001 0.214800000000001 -4.12000000000002E-02
6 -0.425800000000001 0.270000000000002 0.289300000000002
6 -0.4699 0.192100000000001 0.291300000000003
6 -0.448200000000002 0.151600000000001 0.201100000000003
6 -0.391900000000001 0.205800000000001 0.150400000000002
6 -0.377199999999999 0.277700000000001 0.204200000000001
6 0.371200000000003 0.371500000000001 3.78999999999997E-02
6 0.466800000000001 0.395600000000001 6.02999999999994E-02
6 0.479200000000002 0.415100000000001 0.160399999999999
6 0.389000000000003 0.399800000000002 0.2038
6 0.323400000000002 0.373200000000002 0.1254
6 -0.131099999999999 7.18000000000009E-02 0.264000000000002
6 -3.17999999999996E-02 4.95999999999998E-02 0.280500000000002
6 2.03000000000009E-02 0.1205 0.3087
6 -4.26999999999992E-02 0.1856 0.3123
6 -0.136999999999999 0.157300000000001 0.282100000000002
6 -0.139200000000002 0.122600000000001 -0.397700000000001
6 -0.204500000000001 7.05000000000018E-02 -0.437500000000001
6 -0.2513 0.102000000000001 0.487500000000003
6 -0.220299999999998 0.180300000000001 0.4749
6 -0.147600000000001 0.193200000000001 -0.453700000000001
17 0.401420000000003 0.173630000000001 -1.59000000000071E-03
17 0.298100000000001 0.187660000000001 0.212169999999999
17 -7.69199999999993E-02 -7.14200000000019E-02 0.461090000000003
1 0.273089688983731 -4.09232979290994E-04 0.244596011600325
1 0.135719972999218 -5.72977562626403E-02 0.132122168971967
1 0.194824935088667 -7.10944550091356E-02 -4.07838061625084E-02
1 0.3909801111141 -1.19907791742668E-02 -2.43407126910771E-02
1 0.420870034723089 2.33013796911792E-02 0.146898106688273
1 0.175323958480591 0.113218705547431 -0.164073298358102
1 6.80696322919189E-02 3.37476397130587E-02 -0.070157509230266
1 2.68941353777544E-02 0.115138967103294 9.87996417952357E-02
1 0.116123922627686 0.249950626795976 9.85122798686964E-02
1 0.214016756164715 0.265360108555881 -5.47585695653377E-02
1 -0.422917356303134 0.308144096550747 0.350515786054236
1 -0.517272190743566 0.175817601153788 0.346979941452485
1 -0.484007207908489 0.100055333744494 0.174959067324597
1 -0.373741354944225 0.184329847799702 8.08707319681494E-02
1 -0.327017746086864 0.324441367486639 0.196501257236516
1 0.342237594862901 0.352142363875008 -2.85994627323493E-02
1 0.523396190878484 0.3950172148054 1.05952959395849E-02
1 0.545195253222763 0.432878667317023 0.188774338647056
1 0.368830324786471 0.41165655062903 0.27599821240588
1 0.250567674089728 0.359853007837876 0.123428931541211
1 -0.176950178815538 2.52257226844228E-02 0.241207770881596
1 -1.66217037560587E-02 -1.03853386183234E-02 0.259511114321381
1 9.07110649291872E-02 0.137558641893006 0.323091140424792
1 -3.84991157781261E-02 0.246253940059025 0.33572606848988
1 -0.205147996344924 0.18304194815821 0.284160476897504
1 -9.29252862279276E-02 0.112572367841798 -0.339011125722109
1 -0.212168327288039 1.23369006591873E-02 -0.407007108821193
1 -0.317446698739097 8.55091371315703E-02 0.458391251183944
1 -0.244183300764322 0.240555778991524 0.468897798032383
1 -0.115533238161498 0.248263772552193 -0.433386832037562
MODISYMM
12
1 1
2 2
3 1
4 2
5 1
6 2
7 1
8 2
9 1
10 2
11 1
12 2
OPTGEOM
END
BASISSET
SOLDEF2MSVP
DFT
SPIN
PBESOL03C
END
SHRINK
0 2
2 2 2
MAXCYCLE
300
THREDIIS
0.01
FMIXING
98
ATOMSPIN
12
1 1
2 -1
3 1
4 -1
5 1
6 -1
7 1
8 -1
9 1
10 -1
11 1
12 -1
FDOCCUP
2
1 8 3
0 0 0 1 0
0 0 0 0 0
2 8 3
0 0 0 0 0
0 0 0 1 0
TOLINTEG
8 8 8 8 16
MULPOPAN
EXCHSIZE
30000000
BIPOSIZE
30000000
END
At the end of the calculation, compare the final optimized lattice parameters at different levels of theory with the experimental ones (a = 13.422, b= 15.666, c= 13.083, beta= 94.21) to verify their agreement and take note of the final energy that will be needed to calculate the cohesion energy.
Note:this calculation is very time consuming, so in case you cannot run it, precalculated output is provided (p21c.out).
Extraction of molecular building unit
In order to calculate the cohesion energy of a molecular crystal, it is necessary to compute the total energy of the building unit, that is simply the energy of the extracted molecule recognized in the cell, without relaxing it.
Input:
P21/c – extr. molecule
EXTERNAL
RAYCOV
2
22 1.8
17 1.3
MOLECULE
1
1 0 0 0
MODISYMM
2
1 1
24 2
BASISSET
SOLDEF2MSVP
DFT
SPIN
PBESOL03C
END
MAXCYCLE
300
THREDIIS
0.01
FMIXING
98
ATOMSPIN
2
1 1
24 -1
FDOCCUP
2
1 8 3
0 0 0 1 0
0 0 0 0 0
24 8 3
0 0 0 0 0
0 0 0 1 0
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Optimization of molecular building unit
In this case, we will use the same CRYSTAL input used for molecule extraction, with the addition of OPTGEOM keyword.
Input:
P21/c – opt molecule
EXTERNAL
…
OPTGEOM
END
…
Cohesion energy calculation
Now that we have all the ingredients, we can calculate cohesion energy for P21/c crystal.
Calculate the binding energy (Ebinding = Ecrystal/n – Emolecule), the relaxation energy (Erelax = Eoptmolecule – Emolecule) and the final cohesion energy according to the formula reported above.