|
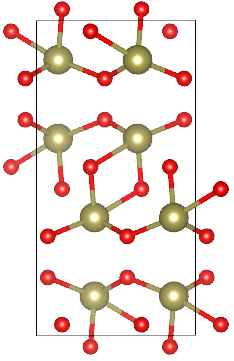
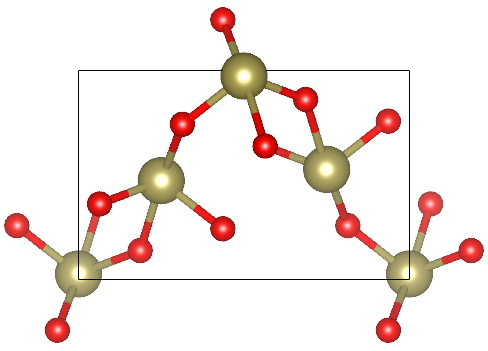
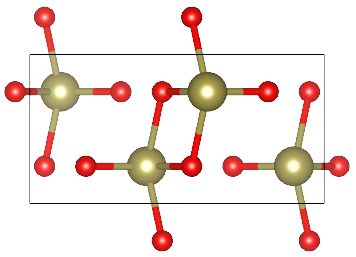
TeO2 allotropes
|
TeO2 is an important substance synthesized via Chemical Vapor Transport (CVT). There are three crystalline phases of TeO2. These are paratellurite alpha-TeO2 (space group P41212), the tellurite beta-TeO2 (space group Pbca), and gamma-TeO2 (space group P21212). The TeO2 phases are described as different arrangements of corner-sharing TeO4 units including two longer Te–O bonds and two shorter ones. The alpha-TeO2 is thermodynamically stable, but naturally the TeO2 is mostly found in beta phase. In this tutorial, we are going to characterize alpha, beta and gamma phases of TeO2, by optimizing their geometries with different basis sets and DFT functionals, simulating one-electron properties as band structure and density of states and their vibrational spectra – IR and Raman. In the end, we will evaluate the relative stability of the three investigated oxides. Similar analyses can be performed for several other compounds of interest synthesized with CVT technique:
- AlF3
- AuCl
- BaCl2, BaBr2
- CaCl2
- CoCl2, CoBr2
- CrCl2, CrCl3, CrBr3, CrI2
- CuCl2
- FeF3, FeCl2, FeI2
- IrBr3, IrI3
- MgF2, MgCl2
- MnCl2
- MoCl2, MoCl3, MoBr3, MoI2
- NaCl
- Nb6F15, Nb3I8
- NiCl2, NiBr2, NiI2
- OsCl4
- PdCl2
- PtCl2, PtCl3
- RhCl3
- RuCl3, RuBr3
- ScF3, ScCl3, ScBr3
- SrCl2, SrBr2
- Ta6Cl15
- TiF3, TiCl3, TiBr3
- VCl2, VCl3, VI2, VI3
- WI3
- YBr3, YI3
- ZrCl2
| Alpha phase | Beta phase | Gamma phase |
 |
 |
 |
Alpha-TeO2
Geometry optimization
In this section, we will start optimizing the geometry of alpha-TeO2 with PBE and PBE0 functional, both including and not including dispersion correction, and with TZVP or SVP basis sets for both Te and O.
In the following, sample input for alpha-TeO2 is reported.
P41212 - alpha
CRYSTAL
0 0 0
92
4.8082 7.6120
2
252 0.0268 0.0268 0.0000
8 0.1386 0.2576 0.1862
OPTGEOM
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
In the geometry input section, all information needed to construct the crystal structure of the investigated systems are reported: space group number, minimal set of lattice parameters, number of irreducible atoms in the unit cell followed by their atomic number and fractional coordinates. For Te, ‘252’ atomic number is specified instead of 52 because of the use of pseudopotential basis set. Moreover, full geometry optimization is requested (both atomic coordinates and cell parameters). The adopted basis sets are SVP, while PBE functional is chosen. Tolerances on integrals are set to 10-8 for the first four criteria and 10-16 for the last one (TOLINTEG 8 8 8 8 16). The convergence criterion on energy for SCF is set to 10-10 (TOLDEE 10). Furthermore, Mulliken population analysis is requested (MULPOPAN).
Exercise:
The same kind of calculation can be performed modifying:
- Basis set for both atomic species;
- DFT functional
- utilizing TZVP basis set for Te and O (reported below) at PBE level in order to verify the effect of basis set choice on the results of the calculation;
- utilizing PBE0 and PBE0-D3 (zero damping) functionals with SVP and/or TZVP basis set (the basis set should be always the same to observe just the effect of the functional)
Note: Since these calculations may be quite time consuming, here you can find pre-computed outputs:
- alpha_opt_svp_pbe.out
- alpha_opt_tzvp_pbe.out
- alpha_opt_svp_pbe0.out
- alpha_opt_tzvp_pbe0.out
- alpha_opt_svp_pbe0d3.out
- alpha_opt_tzvp_pbe0d3.out
Here, we report TZVP basis set for Te and O.
TZVP basis set for O:
8 7
0 0 6 2.0 1.0
27032.382631 0.21726302465E-03
4052.3871392 0.16838662199E-02
922.32722710 0.87395616265E-02
261.24070989 0.35239968808E-01
85.354641351 0.11153519115
31.035035245 0.25588953961
0 0 2 2.0 1.0
12.271113873 0.39768730901
4.9159842006 0.24627849430
0 0 1 0.0 1.0
0.90086482370 1.0000000000
0 1 1 0.0 1.0
0.25000000000 1.0 1.0
0 2 4 4.0 1.0
75.300554155 0.60685103418E-02
17.743733858 0.41912575824E-01
5.5355828651 0.16153841088
2.0685535103 0.35706951311
0 2 1 0.0 1.0
0.78238772422 1.0000000000
0 3 1 0.0 1.0
1.2000000000 1.0000000000
TZVP basis set for Te:
252 13
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 5 2.0 1.0
6213.2001650 0.17392073280E-03
920.89640017 0.11933589842E-02
199.28042708 0.36256556777E-02
24.774233098 -0.59791033012E-01
14.838199169 0.95943203263
0 0 2 2.0 1.0
12.278541238 0.75942429936
6.3806533683 0.35331689542
0 0 1 0.0 1.0
2.2218989571 1.0000000000
0 0 1 0.0 1.0
1.0763427385 1.0000000000
0 0 1 0.0 1.0
0.28557949325 1.0000000000
0 1 1 0.0 1.0
0.11 1.0 1.0
0 2 3 6.0 1.0
204.29400852 0.40605406751E-03
18.208759358 0.60255451613E-01
9.9211024302 -0.27491671277
0 2 3 4.0 1.0
3.1361130985 0.43154849974
1.7187581052 0.55403079110
0.86829668303 0.24087311227
0 2 1 0.0 1.0
0.33815046977 1.0000000000
0 3 6 10.0 1.0
121.51055249 0.63490629024E-03
32.968794396 0.61811936324E-02
19.249862451 -0.88929825218E-02
4.7198407254 0.20159884764
2.3428061416 0.42976049013
1.1135379412 0.38247126751
0 3 1 0.0 1.0
0.49200061510 1.0000000000
0 3 1 0.0 1.0
0.24600030755 1.0000000000
0 4 1 0.0 1.0
0.38255757 1.0000000000
For specifying PBE0-D3(zero damping), please insert in the input:
DFT
PBE0
END
DFTD3
VERSION
3
END
Band structure
Let’s now compute the band structure along a path in the Brillouin zone to characterize the electronic structure of alpha-TeO2. To do so, properties must be run.
Input:
BAND
Path GZARXMG
6 8 120 60 120 1 0
0 0 0 0 0 4
0 0 4 4 4 4
4 4 4 0 4 4
0 4 4 0 4 0
0 4 0 4 4 0
4 4 0 0 0 0
END
In the first line the keyword BAND specifies the one-electron property you want to compute. The second line is the title. Then 7 numbers are specified: the number of segments in the reciprocal space to explore; shrinking factor; total number of k-points along the path; first band to be saved; last band to be saved; plotting option; printing option.
A number of rows follows, equal to the indicated number of segments, that specify the path in the Brillouin zone. To have information about k-points and Brillouin zone of a given space group, have a look at BILBAO Crystallographic server.
Note that the coordinates of the extreme of the segments are all multiplied by the shrinking factor.
To visualize the calculated band structure, you can use Crysplot:
- Select ‘Make a plot’
- Select ‘Band structure plot’
- Import file.25/file.BAND/file.DAT obtained as one of the outputs of the calculation
- Rename k points, change the y axis unit,…
- alpha_band_svp_pbe.BAND
- alpha_band_tzvp_pbe.BAND
- alpha_band_svp_pbe0.BAND
- alpha_band_tzvp_pbe0.BAND
- alpha_band_svp_pbe0d3.BAND
- alpha_band_tzvp_pbe0d3.BAND
Density of states
Another way to have an insight into the electronic structure of a system is computing the density of states, which provides some more information than band structure calculation.
Input:
NEWK
8 8
1 0
DOSS
2 200 60 120 1 14 0
-1 1
-1 5
END
Here we want to calculate density of states projected onto the whole set of atomic orbitals of an indicated atom.
NEWK keyword is inserted to specify the shrinking factor, that could be different from that of previous CRYSTAL calculation. It is needed for the calculation of eigenvectors. 1 and 0 are referred to evaluation of the Fermi level with the new k-points net and printing options, respectively. Keyword DOSS activates the computation of density of states of the investigated system.
7 numbers are specified: number of projections; number of points along the energy axis in which the DOSS is calculated; first band; last band; plot option; degree of the polynomial used for the DOSS expansion; printing option. A number of rows follows, equal to the indicated number of projections, to indicate the projection of all atomic orbitals (-1) of an atom, which is indicated with the correspondent label in the CRYSTAL output.
To visualize the calculated DOSS, you can use Crysplot:
- ‘Make a plot’
- ‘Density of states plot’
- Import file.25 obtained as one of the outputs of the calculation
- Change the x axis unit, line labels…
Moreover, it is also possible to visualize band structure plot and DOSS plot together:
- ‘Make a plot’
- ‘Unified plot of band structure and density of states’
- Import file.BAND and file.DOSS obtained as one of the outputs of band structure and DOSS calculations, respectively
- Modify plot settings
- alpha_doss_svp_pbe.DOSS
- alpha_doss_tzvp_pbe.DOSS
- alpha_doss_svp_pbe0.DOSS
- alpha_doss_tzvp_pbe0.DOSS
- alpha_doss_svp_pbe0d3.DOSS
- alpha_doss_tzvp_pbe0d3.DOSS
Exercise:
Compute band structure and density of states at all the levels of theory you previously computed the geometry (and therefore, the wave function) – PBE/SVP, PBE/TZVP, PBE0/SVP, PBE0/TZVP, PBE0-D3/SVP, PBE0-D3/TZVP. How is the band structure changing? Is alpha-TeO2 an insulator, a semiconductor or a conductor? How is changing the band gap with the level of theory? How Te and O atomic orbitals contributes to the different bands?
Vibrational spectra
To fully characterize alpha-TeO2, a vibrational analysis should be done.
In this part, we are going to compute IR and Raman spectra of this phase.
The first step for computing a spectrum is the calculation of frequencies and intensities.
Note: these calculations are quite time-demanding, so in the end we provide you precomputed outputs so you can have a look at the computed spectra without going through the whole calculation.
Sample input at PBE/SVP level of theory for calculation of frequencies and IR intensities:
P41212 – alpha – IR
CRYSTAL
0 0 0
92
4.90924187 7.41569976
2
252 1.039363941595E-02 1.039363941595E-02 0.000000000000E+00
8 1.454874019916E-01 2.377687513145E-01 2.027357684227E-01
FREQCALC
INTENS
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Sample input at PBE/SVP level of theory for calculation of frequencies and Raman intensities (just the first part of the input is reported, since basis set and Hamiltonian control sections are identical to previous input):
P41212 – alpha – Raman
CRYSTAL
0 0 0
92
4.90924187 7.41569976
2
252 1.039363941595E-02 1.039363941595E-02 0.000000000000E+00
8 1.454874019916E-01 2.377687513145E-01 2.027357684227E-01
FREQCALC
INTENS
INTRAMAN
INCPHF
END
END
END
The indicated coordinates of non-equivalent Te and O atoms are the optimized ones at the same level of theory at which we perform the current calculation (basis sets and functional). This is mandatory since we are working within harmonic approximation. FREQCALC is the keyword for frequency calculation, INTENS for IR peak intensities, INTRAMAN for Raman peak intensities and INTCPHF for Raman tensor.
Now, it is possible to compute IR and Raman spectra in few seconds starting from the results of the previous calculations, specifying just two additional keywords: RESTART and IRPSEC (see inpust reported below). In the folder you are working in there is a file named FREQINFO.DAT/filename.freqinfo that is necessary for the restart.
Here we report just the first part of the inputs, since basis set and Hamiltonian control sections are identical to what previously reported.
Input for IR spectra at PBE/SVP level of theory:
P41212 – alpha – IRSPEC
CRYSTAL
0 0 0
92
4.90924187 7.41569976
2
252 1.039363941595E-02 1.039363941595E-02 0.000000000000E+00
8 1.454874019916E-01 2.377687513145E-01 2.027357684227E-01
FREQCALC
RESTART
INTENS
IRSPEC
END
END
END
Input for Raman spectra at PBE/SVP level of theory:
P41212 – alpha – RAMSPEC
CRYSTAL
0 0 0
92
4.90924187 7.41569976
2
252 1.039363941595E-02 1.039363941595E-02 0.000000000000E+00
8 1.454874019916E-01 2.377687513145E-01 2.027357684227E-01
FREQCALC
RESTART
INTENS
INTRAMAN
RAMSPEC
END
END
END
At the end of these calculations, you will find in the folders two additional outputs: filename.out and IRSPEC.DAT/RAMSPEC.DAT. The first one is useful to observe the vibrational modes of the molecule at ‘Crysplot’ → ‘Make a plot’ → ‘Vibrational spectra & animations’; the second one is useful to visualize and save the IR/Raman spectrum at ‘Crysplot’ → ‘Make a plot’ → ‘Infrared spectra’/’Raman spectra’.
Exercise:
Compute IR and Raman spectra at all levels of theory at which you optimized geometries and compare the results both among each other and respect to the experimental results reported at the bottom of the tutorial. Which level of theory better reproduces the experimental spectra?
Pre-computed outputs:
- alpha_freq_svp_pbe.out
- alpha_irspec_svp_pbe.irspec
- alpha_ramspec_svp_pbe.ramspec
- alpha_freq_tzvp_pbe.out
- alpha_irspec_tzvp_pbe.irspec
- alpha_ramspec_tzvp_pbe.ramspec
- alpha_freq_svp_pbe0.out
- alpha_irspec_svp_pbe0.irspec
- alpha_ramspec_svp_pbe0.ramspec
- alpha_freq_tzvp_pbe0.out
- alpha_irspec_tzvp_pbe0.irspec
- alpha_ramspec_tzvp_pbe0.ramspec
- alpha_freq_svp_pbe0d3.out
- alpha_irspec_svp_pbe0d3.irspec
- alpha_ramspec_svp_pbe0d3.ramspec
- alpha_freq_tzvp_pbe0d3.out
- alpha_irspec_svp_pbe0d3.irspec
- alpha_ramspec_svp_pbe0d3.ramspec
Beta-TeO2
Geometry optimization
In this section, we will start optimizing the geometry of beta-TeO2 with the same basis sets and functionals exploited for alpha phase.
In the following, sample input for beta-TeO2 is reported.
Pbca - beta
CRYSTAL
0 0 0
61
5.464 5.607 12.035
3
252 0.0255 0.3781 0.3818
8 0.137 0.178 0.027
8 0.222 0.086 0.326
OPTGEOM
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Except for geometry specification part, that is related to the specific TeO2 phase to be investigated, the sample input is the same one reported for alpha-TeO2 in previous section.
Exercise:
The same kind of calculation can be performed modifying:
- Basis set for both atomic species;
- DFT functional
- utilizing TZVP basis set for Te and O (already reported) at PBE level in order to verify the effect of basis set choice on the results of the calculation;
- utilizing PBE0 and PBE0-D3 (zero damping) functionals with SVP and/or TZVP basis set (the basis set should be always the same to observe just the effect of the functional)
Note: Since these calculations may be quite time consuming, here you can find pre-computed outputs:
- beta_opt_svp_pbe.out
- beta_opt_tzvp_pbe.out
- beta_opt_svp_pbe0.out
- beta_opt_tzvp_pbe0.out
- beta_opt_svp_pbe0d3.out
- beta_opt_tzvp_pbe0d3.out
Band structure
Let’s now compute the band structure along a path in the Brillouin zone to characterize the electronic structure of beta-TeO2. To do so, properties must be run.
Input:
BAND
Path
8 8 120 120 200 1 0
0 0 0 4 0 0
4 0 0 4 0 4
4 0 4 0 0 4
0 0 4 0 4 4
0 4 4 4 4 4
4 4 4 4 4 0
4 4 0 0 4 0
0 4 0 0 0 0
END
Density of states
Another way to have an insight into the electronic structure of a system is computing the density of states, which provides some more information than band structure calculation.
Input:
NEWK
8 8
1 0
DOSS
2 200 120 200 1 14 0
-1 1
-1 9
END
Exercise:
As already done for alpha-TeO2, compute band structure and density of states at all the levels of theory you previously computed the geometry (and therefore, the wave function) – PBE/SVP, PBE/TZVP, PBE0/SVP, PBE0/TZVP, PBE0-D3/SVP, PBE0-D3/TZVP. How is the band structure changing? Is beta-TeO2 an insulator, a semiconductor or a conductor? How is changing the band gap with the level of theory? How Te and O atomic orbitals contributes to the different bands?
In case you were unable to perform the optimization calculation and could not obtain the file.f9 required for the properties calculation, below we provide you the required files for band structure and density of states visualisation:
- beta_band_svp_pbe.BAND
- beta_band_tzvp_pbe.BAND
- beta_band_svp_pbe0.BAND
- beta_band_tzvp_pbe0.BAND
- beta_band_svp_pbe0d3.BAND
- beta_band_tzvp_pbe0d3.BAND
- beta_doss_svp_pbe.DOSS
- beta_doss_tzvp_pbe.DOSS
- beta_doss_svp_pbe0.DOSS
- beta_doss_tzvp_pbe0.DOSS
- beta_doss_svp_pbe0d3.DOSS
- beta_doss_tzvp_pbe0d3.DOSS
Vibrational spectra
To fully characterize beta-TeO2, a vibrational analysis should be done.
In this part, we are going to compute IR and Raman spectra of this phase.
The first step for computing a spectrum is the calculation of frequencies and intensities.
Note: these calculations are quite time-demanding, so in the end we provide you precomputed outputs so you can have a look at the computed spectra without going through the whole calculation.
Sample input at PBE/SVP level of theory for calculation of frequencies and IR intensities:
beta – IR
CRYSTAL
0 0 0
61
5.43825 5.79683 11.51089
3
252 1.309553564836E-02 3.642054962640E-01 3.747508966839E-01
8 1.531039018545E-01 1.603646688762E-01 3.500041850892E-02
8 2.186512503944E-01 7.063420036329E-02 3.152514649589E-01
FREQCALC
INTENS
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Sample input at PBE/SVP level of theory for calculation of frequencies and Raman intensities (just the first part of the input is reported, since basis set and Hamiltonian control sections are identical to previous input):
beta – IR
CRYSTAL
0 0 0
61
5.43825 5.79683 11.51089
3
252 1.309553564836E-02 3.642054962640E-01 3.747508966839E-01
8 1.531039018545E-01 1.603646688762E-01 3.500041850892E-02
8 2.186512503944E-01 7.063420036329E-02 3.152514649589E-01
FREQCALC
INTENS
INTRAMAN
INCPHF
END
END
END
The indicated coordinates of non-equivalent Te and O atoms are the optimized ones at the same level of theory at which we perform the current calculation (basis sets and functional). This is mandatory since we are working within harmonic approximation. FREQCALC is the keyword for frequency calculation, INTENS for IR peak intensities, INTRAMAN for Raman peak intensities and INTCPHF for Raman tensor.
Now, it is possible to compute IR and Raman spectra in few seconds starting from the results of the previous calculations, specifying just two additional keywords: RESTART and IRPSEC (see inpust reported below). In the folder you are working in there is a file named FREQINFO.DAT/filename.freqinfo that is necessary for the restart.
Here we report just the first part of the inputs, since basis set and Hamiltonian control sections are identical to what previously reported.
Input for IR spectra at PBE/SVP level of theory:
beta – IR
CRYSTAL
0 0 0
61
5.43825 5.79683 11.51089
3
252 1.309553564836E-02 3.642054962640E-01 3.747508966839E-01
8 1.531039018545E-01 1.603646688762E-01 3.500041850892E-02
8 2.186512503944E-01 7.063420036329E-02 3.152514649589E-01
FREQCALC
RESTART
INTENS
IRSPEC
END
END
END
Input for Raman spectra at PBE/SVP level of theory:
beta – IR
CRYSTAL
0 0 0
61
5.43825 5.79683 11.51089
3
252 1.309553564836E-02 3.642054962640E-01 3.747508966839E-01
8 1.531039018545E-01 1.603646688762E-01 3.500041850892E-02
8 2.186512503944E-01 7.063420036329E-02 3.152514649589E-01
FREQCALC
RESTART
INTENS
INTRAMAN
RAMSPEC
END
END
END
At the end of these calculations, you will find in the folders two additional outputs: filename.out and IRSPEC.DAT/RAMSPEC.DAT. The first one is useful to observe the vibrational modes of the molecule at ‘Crysplot’ → ‘Make a plot’ → ‘Vibrational spectra & animations’; the second one is useful to visualize and save the IR/Raman spectrum at ‘Crysplot’ → ‘Make a plot’ → ‘Infrared spectra’/’Raman spectra’.
Exercise:
Compute IR and Raman spectra at all levels of theory at which you optimized geometries and compare the results both among each other and respect to the experimental results reported at the bottom of the tutorial. Which level of theory better reproduces the experimental spectra?
Pre-computed outputs:
- beta_freq_svp_pbe.out
- beta_irspec_svp_pbe.irspec
- beta_ramspec_svp_pbe.ramspec
- beta_freq_tzvp_pbe.out
- beta_irspec_tzvp_pbe.irspec
- beta_ramspec_tzvp_pbe.ramspec
- beta_freq_svp_pbe0.out
- beta_irspec_svp_pbe0.irspec
- beta_ramspec_svp_pbe0.ramspec
- beta_freq_tzvp_pbe0.out
- beta_irspec_tzvp_pbe0.irspec
- beta_ramspec_tzvp_pbe0.ramspec
- beta_freq_svp_pbe0d3.out
- beta_irspec_svp_pbe0d3.irspec
- beta_ramspec_svp_pbe0d3.ramspec
- beta_freq_tzvp_pbe0d3.out
- beta_irspec_svp_pbe0d3.irspec
- beta_ramspec_svp_pbe0d3.ramspec
Gamma-TeO2
Geometry optimization
In this section, we will start optimizing the geometry of gamma-TeO2 with the same basis sets and functionals exploited for alpha and beta phases.
In the following, sample input for gamma-TeO2 is reported.
P21212 - gamma
CRYSTAL
0 0 0
19
4.3433 4.8809 8.5668
3
252 0.13698 0.03024 0.10122
8 0.1778 0.2296 0.2822
8 0.7347 0.1398 0.0379
OPTGEOM
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Exercise:
The same kind of calculation can be performed modifying:
- Basis set for both atomic species;
- DFT functional
- utilizing TZVP basis set for Te and O (already reported) at PBE level in order to verify the effect of basis set choice on the results of the calculation;
- utilizing PBE0 and PBE0-D3 (zero damping) functionals with SVP and/or TZVP basis set (the basis set should be always the same to observe just the effect of the functional)
Note: Since these calculations may be quite time consuming, here you can find pre-computed outputs:
- gamma_opt_svp_pbe.out
- gamma_opt_tzvp_pbe.out
- gamma_opt_svp_pbe0.out
- gamma_opt_tzvp_pbe0.out
- gamma_opt_svp_pbe0d3.out
- gamma_opt_tzvp_pbe0d3.out
Band structure
Let’s now compute the band structure along a path in the Brillouin zone to characterize the electronic structure of gamma-TeO2. To do so, properties must be run.
Input:
BAND
Path
8 8 120 60 120 1 0
0 0 0 4 0 0
4 0 0 4 0 4
4 0 4 0 0 4
0 0 4 0 4 4
0 4 4 4 4 4
4 4 4 4 4 0
4 4 0 0 4 0
0 4 0 0 0 0
END
Density of states
Another way to have an insight into the electronic structure of a system is computing the density of states, which provides some more information than band structure calculation.
Input:
NEWK
8 8
1 0
DOSS
2 200 60 120 1 14 0
-1 1
-1 5
END
Exercise:
As already done for alpha- and beta-TeO2, compute band structure and density of states at all the levels of theory you previously computed the geometry (and therefore, the wave function) – PBE/SVP, PBE/TZVP, PBE0/SVP, PBE0/TZVP, PBE0-D3/SVP, PBE0-D3/TZVP. How is the band structure changing? Is gamma-TeO2 an insulator, a semiconductor or a conductor? How is changing the band gap with the level of theory? How Te and O atomic orbitals contributes to the different bands?
In case you were unable to perform the optimization calculation and could not obtain the file.f9 required for the properties calculation, below we provide you the required files for band structure and density of states visualisation:
- gamma_band_svp_pbe.BAND
- gamma_band_tzvp_pbe.BAND
- gamma_band_svp_pbe0.BAND
- gamma_band_tzvp_pbe0.BAND
- gamma_band_svp_pbe0d3.BAND
- gamma_band_tzvp_pbe0d3.BAND
- gamma_doss_svp_pbe.DOSS
- gamma_doss_tzvp_pbe.DOSS
- gamma_doss_svp_pbe0.DOSS
- gamma_doss_tzvp_pbe0.DOSS
- gamma_doss_svp_pbe0d3.DOSS
- gamma_doss_tzvp_pbe0d3.DOSS
Vibrational spectra
To fully characterize gamma-TeO2, a vibrational analysis should be done.
In this part, we are going to compute IR and Raman spectra of this phase.
The first step for computing a spectrum is the calculation of frequencies and intensities.
Note: these calculations are quite time-demanding, so in the end we provide you precomputed outputs so you can have a look at the computed spectra without going through the whole calculation.
Sample input at PBE/SVP level of theory for calculation of frequencies and IR intensities:
gamma – IR
CRYSTAL
0 0 0
19
4.07768128 5.34299746 8.05502583
3
252 2.498992150715E-01 2.765514529402E-02 1.030133498774E-01
8 2.499194387128E-01 2.094887942168E-01 3.096944651091E-01
8 -2.500308253985E-01 1.540700372590E-01 5.012309092224E-02
FREQCALC
INTENS
END
END
252 9
INPUT
24. 0 2 4 4 2 0
16.814473 281.045843 0
8.793526 61.620656 0
14.877801 67.449464 0
14.269731 134.904304 0
8.724435 14.689547 0
8.291515 29.415063 0
15.205008 35.432057 0
15.225848 53.135687 0
6.071769 9.069802 0
5.804760 13.122304 0
15.206168 -15.745450 0
15.201702 -20.742448 0
0 0 6 2.0 1.0
396.47954659 0.26307731203E-02
21.919773309 -0.13203517066
18.061271390 0.36203197834
8.1403463241 -0.75591120276
2.0705998798 0.79192928400
0.97715185085 0.40558342540
0 0 2 2.0 1.0
11.125986670 -0.15212984183E-01
1.5909401508 0.35202140517
0 0 1 0.0 1.0
0.28232414005 1.0000000000
0 1 1 0.0 1.0
0.12 1.0 1.0
0 2 4 6.0 1.0
17.479502221 0.11517799182
10.433943171 -0.41205302672
1.3623024763 0.78760578076
0.59239616258 0.15283299018
0 2 1 4.0 1.0
2.7943903068 1.0000000000
0 2 1 0.0 1.0
0.34478160137 1.0000000000
0 3 5 10.0 1.0
50.821835991 0.33763474774E-02
18.884095378 -0.35221408938E-02
4.2527304630 0.28254216065
1.8757557092 0.52039372916
0.77069282849 0.32213541689
0 3 1 0.0 1.0
0.25000000000 1.0000000000
8 5
0 0 5 2.0 1.0
2266.1767785 -0.53431809926E-02
340.87010191 -0.39890039230E-01
77.363135167 -0.17853911985
21.479644940 -0.46427684959
6.6589433124 -0.44309745172
0 0 1 2.0 1.0
0.84197953374 1.00000000000
0 1 1 0.0 1.0
0.28000000000 1.0 1.0
0 2 3 4.0 1.0
17.808254450 0.43394573193E-01
3.8854243945 0.23094120765
1.0579384045 0.51375311064
0 3 1 0.0 1.0
1.2000000000 1.00000000000
99 0
END
DFT
PBE
END
SHRINK
8 8
TOLDEE
10
TOLINTEG
8 8 8 8 16
MULPOPAN
END
Sample input at PBE/SVP level of theory for calculation of frequencies and Raman intensities (just the first part of the input is reported, since basis set and Hamiltonian control sections are identical to previous input):
gamma – IR
CRYSTAL
0 0 0
19
4.07768128 5.34299746 8.05502583
3
252 2.498992150715E-01 2.765514529402E-02 1.030133498774E-01
8 2.499194387128E-01 2.094887942168E-01 3.096944651091E-01
8 -2.500308253985E-01 1.540700372590E-01 5.012309092224E-02
FREQCALC
INTENS
INTRAMAN
INCPHF
END
END
END
The indicated coordinates of non-equivalent Te and O atoms are the optimized ones at the same level of theory at which we perform the current calculation (basis sets and functional). This is mandatory since we are working within harmonic approximation. FREQCALC is the keyword for frequency calculation, INTENS for IR peak intensities, INTRAMAN for Raman peak intensities and INTCPHF for Raman tensor.
Now, it is possible to compute IR and Raman spectra in few seconds starting from the results of the previous calculations, specifying just two additional keywords: RESTART and IRPSEC (see inpust reported below). In the folder you are working in there is a file named FREQINFO.DAT/filename.freqinfo that is necessary for the restart.
Here we report just the first part of the inputs, since basis set and Hamiltonian control sections are identical to what previously reported.
Input for IR spectra at PBE/SVP level of theory:
gamma – IR
CRYSTAL
0 0 0
19
4.07768128 5.34299746 8.05502583
3
252 2.498992150715E-01 2.765514529402E-02 1.030133498774E-01
8 2.499194387128E-01 2.094887942168E-01 3.096944651091E-01
8 -2.500308253985E-01 1.540700372590E-01 5.012309092224E-02
FREQCALC
RESTART
INTENS
IRSPEC
END
END
END
Input for Raman spectra at PBE/SVP level of theory:
gamma – IR
CRYSTAL
0 0 0
19
4.07768128 5.34299746 8.05502583
3
252 2.498992150715E-01 2.765514529402E-02 1.030133498774E-01
8 2.499194387128E-01 2.094887942168E-01 3.096944651091E-01
8 -2.500308253985E-01 1.540700372590E-01 5.012309092224E-02
FREQCALC
RESTART
INTENS
INTRAMAN
RAMSPEC
END
END
END
At the end of these calculations, you will find in the folders two additional outputs: filename.out and IRSPEC.DAT/RAMSPEC.DAT. The first one is useful to observe the vibrational modes of the molecule at ‘Crysplot’ → ‘Make a plot’ → ‘Vibrational spectra & animations’; the second one is useful to visualize and save the IR/Raman spectrum at ‘Crysplot’ → ‘Make a plot’ → ‘Infrared spectra’/’Raman spectra’.
Exercise:
Compute IR and Raman spectra at all levels of theory at which you optimized geometries and compare the results both among each other and respect to the experimental results reported at the bottom of the tutorial. Which level of theory better reproduces the experimental spectra?
Note: Since these calculations may be quite time consuming, here you can find pre-computed outputs:
- gamma_freq_svp_pbe.out
- gamma_irspec_svp_pbe.irspec
- gamma_ramspec_svp_pbe.ramspec
- gamma_freq_tzvp_pbe.out
- gamma_irspec_tzvp_pbe.irspec
- gamma_ramspec_tzvp_pbe.ramspec
- gamma_freq_svp_pbe0.out
- gamma_irspec_svp_pbe0.irspec
- gamma_ramspec_svp_pbe0.ramspec
- gamma_freq_tzvp_pbe0.out
- gamma_irspec_tzvp_pbe0.irspec
- gamma_ramspec_tzvp_pbe0.ramspec
- gamma_freq_svp_pbe0d3.out
- gamma_irspec_svp_pbe0d3.irspec
- gamma_ramspec_svp_pbe0d3.ramspec
- gamma_freq_tzvp_pbe0d3.out
- gamma_irspec_svp_pbe0d3.irspec
- gamma_ramspec_svp_pbe0d3.ramspec
Experimental spectra
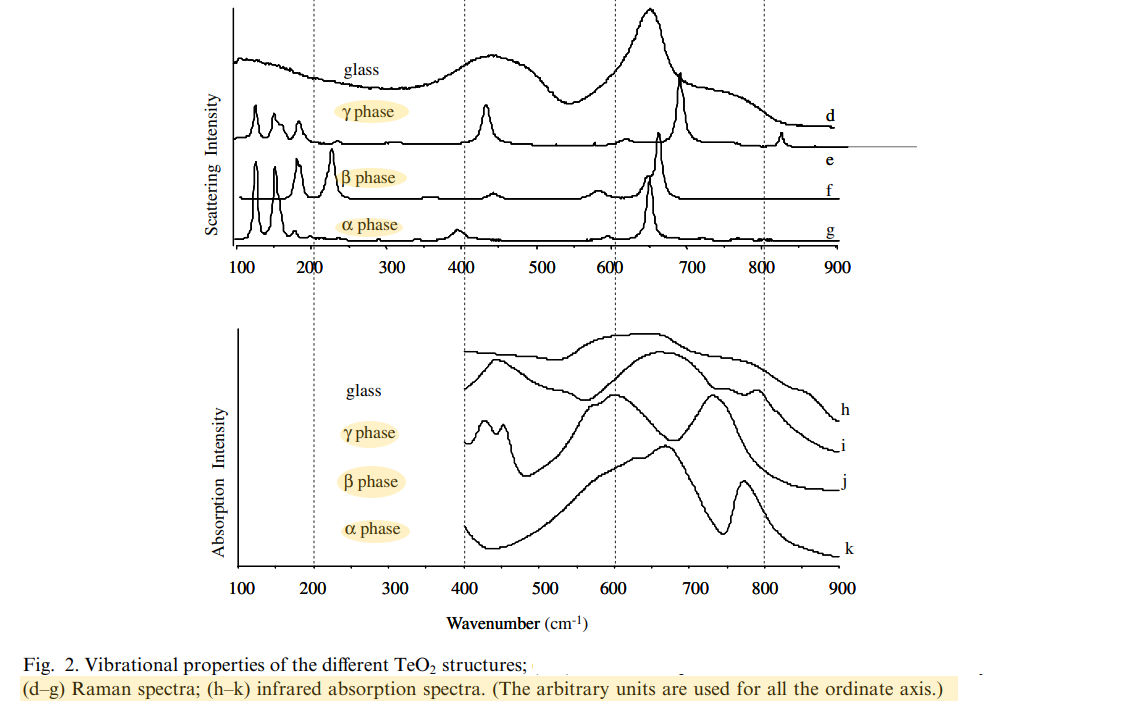
Relative stability
With the calculations completed so far, we can now determine the relative stability of the three allotropes under consideration at different levels of theory. This will be achieved by comparing the internal energy of the three systems, derived from geometry optimization, along with the Gibbs free energy (EL+E0+ET+PV-TS) obtained from vibrational analysis. Here we will just report the result obtained at PBE0-D3/TZVP level of theory. Note that these quantities are comparable when expressed per unit formula, so be sure to divide the relevant values from the outputs accordingly.
| Alpha-TeO2 | Beta-TeO2 | Gamma-TeO2 | |
| Internal energy (E) | -418.4105 | -418.4102 | -418.4093 |
| Gibbs energy (G) | -418.4067 | -418.4065 | -418.4052 |
From our results, it is possible to observe that alpha-TeO2 is the most stable allotrope - as experimentally observed - with a Δ E of -0.9 kJ/mol and Δ G of -0.5 kJ/mol repsect to beta allotrope,and Δ E of -3.2 kJ/mol and Δ G of -3.9 kJ/mol repsect to gamma one.
Exercise:
Build a table similar to the one reported above and study the relative stability of the three allotropes at different levels of theory (PBE0-D3/SVP; PBE0/TZVP; PBE0/SVP; PBE/TZVP; PBE/SVP)